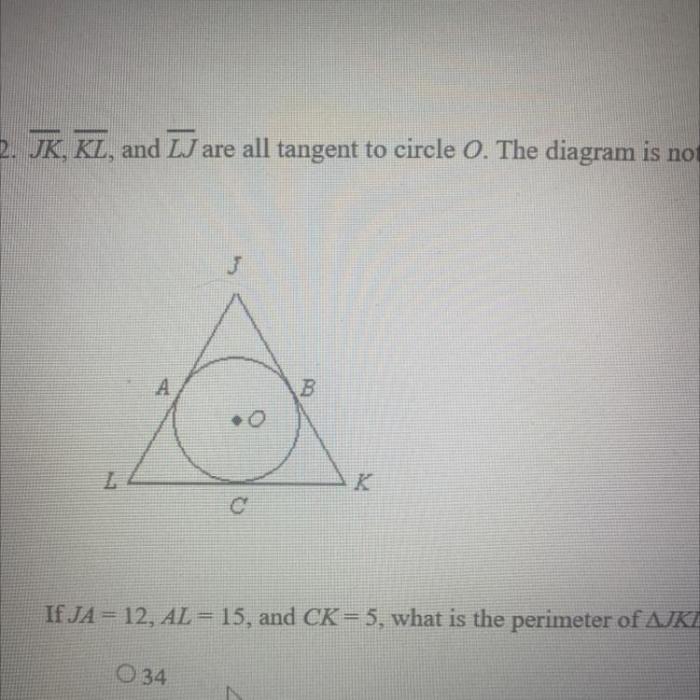
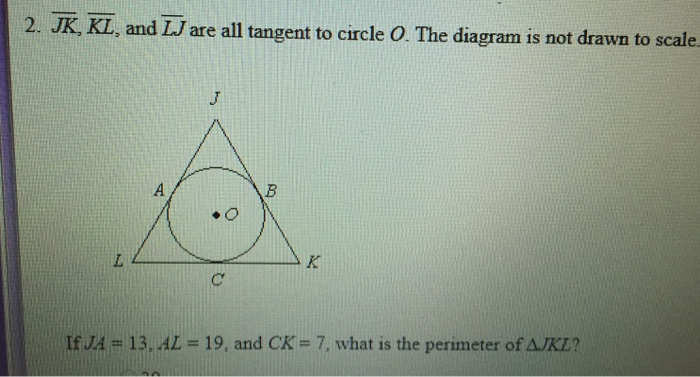
Jk kl and lj are all tangent – In the realm of geometry, where circles and lines dance in harmony, there exists a special connection known as tangency. Enter JK, KL, and LJ—three lines that share a unique relationship with a circle. Join us as we delve into their captivating story of tangency, exploring its properties, constructions, and applications.
Tangency, in essence, occurs when a line intersects a circle at exactly one point, forming a right angle. This seemingly simple concept unlocks a wealth of geometric insights and practical applications.
Definition of Tangency
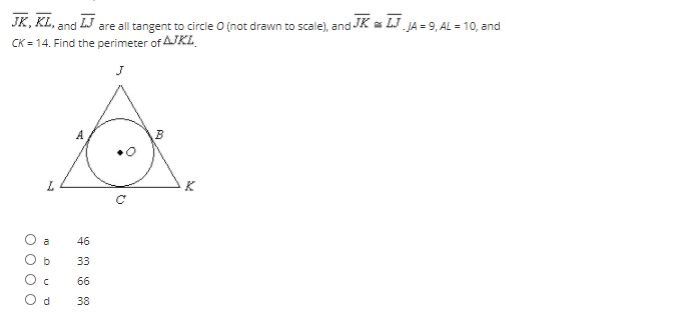
In geometry, tangency refers to the relationship between two geometric objects that touch each other at exactly one point. The point of contact is known as the point of tangency.
Exploring the geometric relationship between jk, kl, and lj reveals that they are all tangent to a circle. This concept is integral to understanding the nature of circles and their properties. If you’re seeking further insights into historical events and their impact, check out the apush period 3 leq prompts for an in-depth analysis of pivotal moments in American history.
Returning to the topic of tangents, the interplay between jk, kl, and lj highlights the significance of geometric relationships in shaping our understanding of the world around us.
Properties of Tangent Lines
Tangent lines possess several unique properties:
- Perpendicularity:A tangent line to a circle or curve at a given point is perpendicular to the radius or normal line drawn from the point of tangency.
- Unique Tangent:For any given point on a curve, there is only one tangent line that can be drawn.
- No Intersection:A tangent line and the curve it touches do not intersect at any other point besides the point of tangency.
Examples of Tangent Lines
Tangent lines have numerous applications in real-world scenarios:
- Engineering:Tangent lines are used in the design of bridges, roads, and other structures to ensure smooth transitions and optimal angles.
- Physics:Tangent lines are used to calculate the trajectory of projectiles, such as a ball thrown in the air or a rocket launched into space.
- Geometry:Tangent lines are used to construct and analyze geometric shapes, such as circles, parabolas, and ellipses.
Identifying Tangent Lines
Identifying tangent lines to a circle is a fundamental concept in geometry. A tangent line is a line that intersects the circle at exactly one point, called the point of tangency. Understanding the conditions for tangency is crucial for various applications, such as finding the slope of a tangent line or constructing circles tangent to other geometric figures.
Conditions for Tangency
- A line is tangent to a circle if and only if the line is perpendicular to the radius of the circle at the point of tangency.
- The radius of the circle drawn to the point of tangency is perpendicular to the tangent line.
- The distance from the center of the circle to the tangent line is equal to the radius of the circle.
Role of the Radius of the Circle
The radius of the circle plays a vital role in determining tangency. The distance from the center of the circle to any point on the tangent line is equal to the radius of the circle. This property is essential for identifying tangent lines and constructing circles tangent to other figures.
Method for Identifying Tangent Lines
To identify a tangent line to a given circle:
- Draw a radius from the center of the circle to the point of tangency.
- Draw a line perpendicular to the radius at the point of tangency.
- The line drawn in step 2 is the tangent line to the circle.
Constructions Involving Tangents: Jk Kl And Lj Are All Tangent
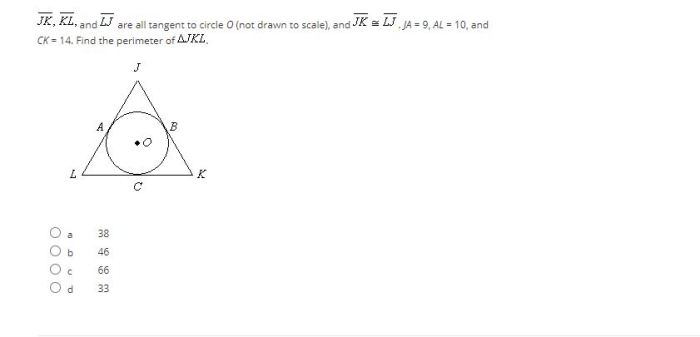
Constructions involving tangents play a significant role in geometry, enabling us to draw tangent lines to circles from various points.
Constructing a Tangent Line from a Given Point
To construct a tangent line to a circle from a given point, follow these steps:
- Draw a line segment from the given point to the center of the circle.
- Draw a radius perpendicular to the line segment at the point where it intersects the circle.
- The line passing through the given point and perpendicular to the radius is the tangent line.
Constructing Two Tangent Lines from a Point Outside the Circle
To construct two tangent lines to a circle from a given point outside the circle, follow these steps:
- Draw a line segment from the given point to the center of the circle.
- Extend the line segment past the center to form a diameter.
- Draw a line perpendicular to the diameter at the point where it intersects the circle.
- The two lines passing through the given point and tangent to the circle are the two tangent lines.
Summary of Tangent Constructions
| Construction | Description |
|---|---|
| Tangent from a given point | Draw a perpendicular from the point to the circle’s radius at the point of intersection. |
| Two tangents from a point outside the circle | Draw a diameter through the point and the circle’s center. Draw a perpendicular from the point to the diameter at the point of intersection. |
Applications of Tangency

Tangency finds extensive applications in various fields, including geometry, physics, and engineering. In geometry, it helps determine segment lengths, prove theorems, and construct geometric figures. In physics, it plays a crucial role in optics, projectile motion, and other areas.
Applications in Geometry
In geometry, tangency is used to:
- Determine the length of a segment:By drawing a tangent to a circle from an external point, we can use the properties of tangents to find the length of the segment joining the point and the point of tangency.
- Prove theorems:Tangency is used in proving various geometric theorems, such as the Pythagorean theorem, the angle bisector theorem, and the inscribed angle theorem.
- Construct geometric figures:Tangency is used in constructing geometric figures, such as inscribed and circumscribed circles, and in drawing parallel and perpendicular lines.
Applications in Physics
In physics, tangency is used in:
- Optics:In optics, the concept of tangency is used to analyze the reflection and refraction of light. Tangent lines are used to determine the angle of incidence, angle of reflection, and angle of refraction, which are essential for understanding the behavior of light.
- Projectile motion:In projectile motion, the trajectory of a projectile is a parabola. The tangent to the parabola at any point gives the direction of motion of the projectile at that instant.
Applications in Engineering and Design
In engineering and design, tangency is used in:
- Architectural design:Tangency is used in architectural design to create curved surfaces, such as domes and arches. Tangent lines are used to determine the curvature and shape of these surfaces.
- Mechanical engineering:In mechanical engineering, tangency is used in the design of gears and other mechanical components. Tangent lines are used to ensure smooth engagement and transmission of motion between gears.
Overall, tangency is a fundamental concept with wide-ranging applications in various fields. Its understanding is essential for solving problems, proving theorems, and designing structures and systems.
Historical Perspectives on Tangency
The concept of tangency has a rich history, dating back to ancient times. It played a significant role in the development of geometry and mathematics as a whole.
One of the earliest known references to tangency can be found in the works of Euclid, a Greek mathematician who lived in the 3rd century BC. In his book “Elements,” Euclid defined a tangent as a line that touches a circle at a single point, without intersecting it.
He also developed a number of theorems related to tangents, including the famous “Tangent-Secant Theorem,” which states that the square of the length of a tangent from a point outside a circle is equal to the product of the lengths of the two secants drawn from the same point.
Archimedes
Archimedes, another Greek mathematician who lived in the 3rd century BC, also made significant contributions to the study of tangency. He developed a method for constructing tangents to circles using a compass and straightedge, and he also proved a number of theorems related to the lengths of tangents and secants.
Archimedes’ work on tangency was later used by Apollonius of Perga, a Greek mathematician who lived in the 2nd century BC, to develop a comprehensive theory of conic sections.
René Descartes
In the 17th century, René Descartes, a French mathematician and philosopher, developed analytic geometry, which allowed mathematicians to use algebra to study geometric figures. This led to a new understanding of tangency, as it became possible to express the equation of a tangent line in terms of the coordinates of the point of tangency.
Significance of Tangency, Jk kl and lj are all tangent
Tangency has played a significant role in the evolution of geometry and mathematics. It is used in a wide variety of applications, including architecture, engineering, and computer graphics. For example, architects use tangents to design curves that are smooth and aesthetically pleasing, while engineers use tangents to calculate the forces acting on objects in motion.
Tangency is also used in computer graphics to create realistic images of curved surfaces.
FAQ
What is the significance of the radius of a circle in determining tangency?
The radius of a circle plays a crucial role in tangency. A line is tangent to a circle if and only if it is perpendicular to the radius drawn to the point of tangency.
How can we construct a tangent line to a circle from a given point outside the circle?
To construct a tangent line from a point outside the circle, draw a line from the point to the center of the circle. Then, construct a perpendicular bisector to this line. The perpendicular bisector will intersect the circle at two points, and the lines connecting these points to the given point will be tangent to the circle.
